Área de um quadrado e retangulo questões de concurso
O quadrado é um quadrilatero (quatro lados ) . E todos os seus lados são congruente (iguais).
Para calcular a área de um quadrado , podemos dizer que A= l²
Retangulo também é um quadrilatero ( tem quatro lados ) e para calcular sua área usamos A=b.h

Exemplo : Calcule a área do quadrado abaixo sabendo que seus lados medem 4 m ?
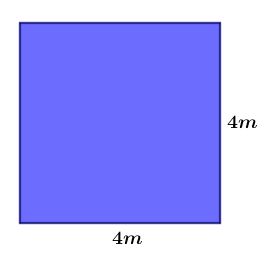
Área = 4²
Área = 4 . 4 = 16m²
Exemplo: (TJ RS 2005 – Officium). Na figura abaixo, estão representados dois quadrados e dois retângulos que, justapostos, formam um quadrado maior.

A área do quadrado menor é 9, e a do quadrado médio é 36. A área do retângulo escurecido A é
a) 12
b) 15
c) 18
d) 24
e) 27
Resposta : Se analisamos bem existe dois quadrados um com área 9 e outro com área 36 , e com isso sabemos que a raiz de 9 = 3 e a de 36 = 6 .
Com isso sabemos que um dos lados mede 3 e outro mede 6 e para achar o valor de A agora ficou facil , usando a formula do retangulo onde Área = b.h = 3.6 = 18 . Então o valor de A = 18 .
Resolução : Quando o quadrado tem uma diagonal , dividimos em dois triangulos isoceles com dois angulos retos. Logo, a diagonal é hipotenusa e os outros dois lados catetos desse triângulo. Sabendo que esses dois lados são iguais, com isso temos que usar o teorema de pitagoras para achar o valor dos lados .
P= 4.L
P=4.6
P=24 cm
Para calcular a área de um quadrado , podemos dizer que A= l²

Retangulo também é um quadrilatero ( tem quatro lados ) e para calcular sua área usamos A=b.h
Exemplo : Calcule a área do quadrado abaixo sabendo que seus lados medem 4 m ?

Área = 4²
Área = 4 . 4 = 16m²
Exemplo: (TJ RS 2005 – Officium). Na figura abaixo, estão representados dois quadrados e dois retângulos que, justapostos, formam um quadrado maior.
A área do quadrado menor é 9, e a do quadrado médio é 36. A área do retângulo escurecido A é
a) 12
b) 15
c) 18
d) 24
e) 27
Resposta : Se analisamos bem existe dois quadrados um com área 9 e outro com área 36 , e com isso sabemos que a raiz de 9 = 3 e a de 36 = 6 .
Com isso sabemos que um dos lados mede 3 e outro mede 6 e para achar o valor de A agora ficou facil , usando a formula do retangulo onde Área = b.h = 3.6 = 18 . Então o valor de A = 18 .
Exemplo:Qual o perímetro de um quadrado que possui uma das diagonais medindo 72 cm?
a) 24 cm
b) 25 cm
c) 28 cm
d) 36 cm
e) 6 cm
Resolução : Quando o quadrado tem uma diagonal , dividimos em dois triangulos isoceles com dois angulos retos. Logo, a diagonal é hipotenusa e os outros dois lados catetos desse triângulo. Sabendo que esses dois lados são iguais, com isso temos que usar o teorema de pitagoras para achar o valor dos lados .
x2 + x2 = 72
2x2 = 72
x2 = 72
2
2
x2 = 36
x = 6 cm.
Achamos o valor do lado do quadrado .P= 4.L
P=4.6
P=24 cm
.jpg)

Comentários
Postar um comentário