Lei dos senos e lei dos cosseno

-
A lei do seno é usada quando o triangulo não é um de (90°) e sim um triangulo qualquer  . Irei mostrar abaixo como usar essa lei no triangulo.
 Formula :

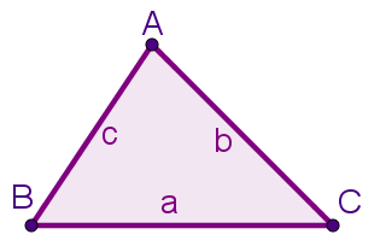
   a    =    b    =    c    
senA    senB    senC 

Exemplos ;
No triângulo a seguir, determine a medida do lado AC, tendo em vista as medidas presentes nele. (Use √2 = 1,4 e √3 = 1,7).

Solução :  Olhando para o triângulo podemos ver que x ta oposto a o ângulo de 45° e 10 oposto a o ângulo de 60°. Agora so montar e resolver  e sempre lembrar da tabela dos ângulos notáveis .


 Exemplo 2  :
(Mackenzie – SP) Três ilhas A, B e C aparecem num mapa em escala 1:10000, como na figura. Das alternativas, a que melhor se aproxima de distância entre as ilhas A e B é:


Solução :
Observando  o segmento AB é oposto ao ângulo C. Somando as medidas internas de um triângulo, concluímos que o ângulo C mede 45°. Os lados que serão usados nesse problema são AC = 12 cm e AB = x. Os ângulos opostos a esses lados são: 30° e 45° então usando a lei de senos para chegar no que queremos . 



Agora a lei do cossenos : É usada em um triângulo qualquer a formula de calcular e é parecida com o teorema de pitagoras .

Exemplo: Determine o valor de y no triângulo obtusângulo abaixo.






Comentários

Postar um comentário

Postagens mais visitadas deste blog

Área de um quadrado e retangulo questões de concurso

-
Imagem
 O quadrado é um quadrilatero (quatro lados ) . E todos os seus lados são congruente (iguais). Para calcular a área de um quadrado , podemos dizer que  A= l²                         Retangulo também é um quadrilatero ( tem quatro lados ) e para calcular sua área usamos A=b.h Exemplo : Calcule a área do quadrado abaixo sabendo que seus lados medem 4 m ? Área = 4² Área = 4 . 4 = 16m² Exemplo: (TJ RS 2005 – Officium). Na figura abaixo, estão representados dois quadrados e dois retângulos que, justapostos, formam um quadrado maior. A área do quadrado menor é 9, e a do quadrado médio é 36. A área do retângulo escurecido A é a) 12 b) 15 c) 18 d) 24 e) 27   Resposta : Se analisamos bem existe dois quadrados um com área 9 e outro com área 36 , e com isso sabemos que a raiz de 9 = 3 e a de 36 = 6 .  Com isso sabemos que um dos lados mede 3 e outro mede 6 e para achar o valor de A agora ficou facil , usando a formula do retangulo onde Área = b.h = 3.6 = 18
Leia mais

Trigonometria no Triangulo retangulo

-
Imagem
-As funções trigonométricas são as funções relacionadas aos triângulos retângulos, que possuem um ângulo de 90°. São elas: seno, cosseno e tangente. As funções trigonométricas estão baseadas nas razões existentes entre dois lados do triângulo em função de um ângulo. Lados do Triângulo Retângulo: Hipotenusa e Catetos Antes de mais nada, temos que saber que no triângulo retângulo, a hipotenusa é o lado oposto ao ângulo reto e o maior lado do triângulo. Já os catetos são os lados adjacentes e que formam o ângulo de 90°. Note que dependendo dos lados de referência ao ângulo, temos o cateto oposto e o cateto adjacente. . -A razão entre eles são . Tabela do ângulos notáveis : Exemplos : 1-Determine os valores de x, y, w e z em cada caso: a) Através do cosseno de 30°, temos: cos 30° = cat. adjacente a 30°                 hipotenusa √ 3 = 16 2       x √ 3 • x = 16 • 2 x = 32      √3 x =  32•√3      √3•√3 x =  32•√3      3 b) Através do seno
Leia mais